Nock is not super complex, and most programmers can learn the basics of it rapidly. The mental model gained by learning Nock turns out to be very useful in learning Hoon and understanding Urbit. While the Urbit docs generally suggest to not worry about Nock, Nock is very simple and small. Most programmers will feel more comfortable in Hoon having learned Nock’s basics. The goal of this tutorial is to explain Nock clearly in terms most programmers will relate to, to impart a feeling of confidence with very basic Nock, and to give a knowledge of Nock’s idioms and big wins so that they carry over to learning Hoon.
This tutorial was originally published online
by ~timluc-miptev in early 2020 and remains
an
excellent exposition of Nock’s affordances.
0 and 1
0, the “Memory
Slot” Function
1, the
“Quoter” Function
4, the
Incrementing Function
3, the Cell
Detector, and 5, the
Equality Tester
2, the
“Subject-Altering” Function
1 (Quoter
Function)
6, “If/Else”
Conditional Branch
7, the
“Composition” Opcode
8, the
“Variable Push” Opcode
9, Run a
Stored Procedure Arm in a Core
10, Replace a
Memory Slot
11, Hints and
Side Effects for the Interpreter
When people first look at Nock, they see the definition, which is fairly intimidating. I’m talking about lines like this:
/[(a + a) b] /[2 /[a b]]
The problem is, the programmer may already know that Nock code looks more like the below – just lists of numbers, with no symbols:
[6 [5 [0 6] [1 0]] [0 7] [9 4 [[0 2] [2 [0 6] [0 5]] [4 0 7]]] 5]
What gives? Which one is the “real” Nock?
We are looking at two different things in the examples above:
Pseudocode for how to interpret Nock.
Code to be interpreted (written as lists of numbers).
The symbols and spec are pseudocode, not real Nock code. They could just as easily be written in English, and they will never be written down as actual Nock code and given to an interpreter. They represent what an interpreter should do to turn Nock code into interpreter instructions.
The lists of numbers are the actual Nock code. This is what you feed to an interpreter to get some result.
An interpreter can be a computer program, or it can be a human manually expanding Nock code into results. In both cases, the program and human have to know the Nock pseudocode in order to do the right thing with incoming Nock code.
So a Nock interpreter is any entity that takes Nock code as input, and gives a noun as output. A noun can be:
:: a number 782 :: a cell (pair with two elements) [782 9872] 5:: each element can itself be a pair [782 [9872 89728]] :: the above can be written as [782 9872 89728]
We will be expanding Nock pseudocode manually in the examples that follow, in effect acting as our own interpreter.
If we want to check that we’re getting the right results from our manual interpretation, we need to run a Nock interpreter, such as the Urbit Dojo.
Start up a Dojo session on a fake ship.1
At the prompt, we can execute Nock using .* dottar,
e.g., .*(NOCK_SUBJECT, NOCK_FORMULA).
Let’s keep this simple:
subject = an argument to a function
formula = the function
That’s it. We’ll see below how this works, going really slowly with examples.
OK, so the interpreter takes two arguments, a “subject" and a “formula". Both are nouns (a number or a cell). Let’s run some insanely simple Nock code in the Dojo:2
> .*(42 [0 1]) 42
In the above, 42 is our subject.
[0 1]
is our formula.
Formulas are always cells, and the first element of the cell is a number that you can think of as the name of the function.
In this case, our function name is 0, which is the memory
slot function. It is always followed by 1 number, in this case 1,
which is the number of the memory slot to fetch in the
subject.
Whenever we look at Nock code, we want to ask:
What is the subject (function argument)? In this
case, it’s 42.
What is the formula (function)? In this case, it’s
[0 1].
What value does that formula (function) produce
when called on this subject (argument)? In this case,
the return value is 42.
Why is the return value 42? How
does this formula
work?
0 and 1The two most basic Nock functions are 0 address and 1
constant. The goal here is to get strong intuitions of what they
do, how they handle edge cases, and how this relates to the
Nock spec/pseudocode.
Before getting started on Nock proper, we should
understand how Nock and Hoon handle addresses in binary
trees. If you already understand why memory slot 5 of
[['apple' %pie] [0b1101 0xdad]]
is %pie, you are
good to go and can skip ahead to Section 2.3.
Every noun in Nock can be thought of as a tree, which means we can give an exact number to access any position in the tree. This means that, no matter how big our subject (argument) is, we can yank a value out of any part of it.
The Nock specification defines noun tree addressing:
/[1 a] a /[2 a b] a /[3 a b] b /[(a + a) b] /[2 /[a b]] 5/[(a + a + 1) b] /[3 /[a b]]
This permits the address to be defined within a particular subtree as well as within the overall tree (Figure 1).

That is, how do you say which slot number you want from a given tree? We say that:
The tree root is address 1.
The head of every node \(n\) is \(2n\).
The tail of every node \(n\) is \(2n+1\).
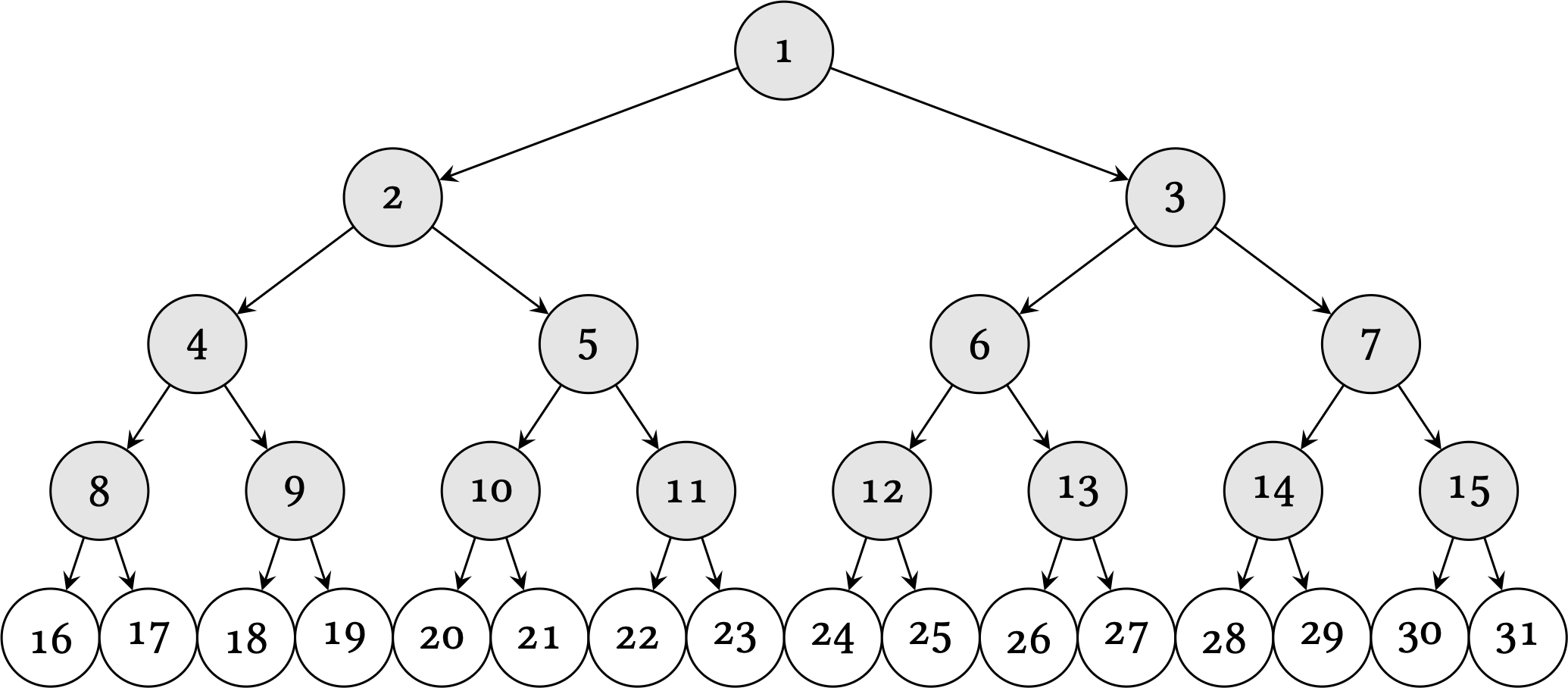
Let’s take an example tree to illustrate. In Nock cell form, the tree is:
[[4 5] [6 14 15]]
Diagrammatically, the tree looks like Figure 2.
1 is the address of the whole tree,
[[4 5] [6 14 15]].
2 is the address of the left branch, [4 5].
3 is the address of the right branch, [6 14 15].
15 is the value 15.
Let’s play around now in the Dojo Nock interpreter so that
we can confirm this. In each example, our subject (argument)
will be the tree [[4 5] [6 14 15]].
:: formula (function) [0 1]: get the whole tree > .*([[4 5] [6 14 15]] [0 1]) [[4 5] 6 14 15] 5:: formula (function) [0 2]: get the left branch > .*([[4 5] [6 14 15]] [0 2]) [4 5] :: formula (function) [0 7]: get the subtree in slot 7 10> .*([[4 5] [6 14 15]] [0 7]) [14 15]
0, the “Memory Slot”
FunctionThe pseudocode for the 0
opcode3
is as follows:
*[a 0 b] /[b a]
/[b a]
is pseudocode. In English, it means “a is a
binary
tree. Get the memory slot numbered b.
So if a were the tree [9 10],
and b were 1, we’d get the
memory slot 1 in the tree [9 10],
which is just the tree
itself.
Written in pseudocode, that’s /[1 [9 10]].
We can
also do /[2 [9 10]],
which grabs memory slot 2, aka
9.
Let’s look at some examples. I’ve put them first in Dojo form so that you can see how they run in that interpreter, and then I show the “human interpreter" in pseudocode below that.
:: get memory slot 1 > .*([50 51] [0 1]) [50 51] :: PSEUDOCODE -- replaces the Dojo's () with [] 5*[[50 51] [0 1]] :: *[a 0 b] -> a = [50 51], b = 1 /[1 [50 51]] [50 51]
> .*([50 51] [0 2]) 50 :: PSEUDOCODE -- replaces the Dojo's () with [] *[[50 51] [0 2]] 5:: *[a 0 b] -> a = [50 51], b = 2 /[2 [50 51]] 50
> .*([50 51] [0 [0 1]]) dojo: hoon expression failed :: PSEUDOCODE *[[50 51] [0 [0 1]]] 5/[[0 1] [50 51]] :: can't evaluate this--a memory slot must be a number like 2, not a cell like [0 1] CRASH
00 is everywhere in
Nock, because “get something from a
memory slot” really means “store stuff in a place and get it
whenever I want,” which is another name for creating
variables. These memory slot numbers take the place of
variable names.
If you’re familiar with assembly or C, they’re conceptually similar to memory pointers or registers in how Nock uses them. Keep in mind though, Nock is functional/immutable, so it doesn’t update memory locations: it creates copies of data structures with altered values.
We’ve also seen that the memory slot function can’t take just anything as the memory slot to fetch: it must receive an atom (number).
1, the “Quoter”
FunctionThis is another really simple function. You can think of it as a “quoter”: it just returns any value passed to it exactly as it is. It ignores the subject, and just quotes the value after it. Let’s look at a couple examples.
> .*([20 30] [1 67]) 67 :: [1 2 587] is same as [1 [2 [587]]] > .*([20 30] [1 [2 [587]) 5[2 587]
It doesn’t matter how much information is after the 1: 1 is
a dumb function that just returns it all.
The pseudocode for 1 is:
*[a 1 b] b
In English, this means: “ignore the subject a, and just
return everything after the 1 exactly as it is.
Let’s look at our first example, .*([20 30] [1 67]).
The subject a is [20 30],
so we ignore that. What’s after the
1? 67, so we return that.
In the second example, “everything after the 1” is
longer, but the same rule applies: the Nock interpreter just
returns it exactly as it is, after stripping out unnecessary
brackets.
11 is a simple
function that just returns whatever is after it
(“quoter” or “constant”). It’s useful for quoting values that
you want to use later in your Nock code.
4, the Incrementing
Function0 and 1 are simple
functions that don’t have any nested
behavior. Now we’re going to move to a function that
does have nested children, opcode 4. In these
examples,
pay attention to how 4 operates on its
arguments; we’ll
look at pseudocode and break down the examples in a
moment.
> .*(50 [4 0 1]) 51 > .*(50 [4 4 0 1]) 552 > .*([100 150] [4 4 0 3]) 152 10> .*(50 [4 1 98]) 99 > .*(50 [4 1 [0 2]]) dojo: hoon expression failed
Here’s 4’s pseudocode,
juxtaposed with that of 0 and
1:
*[a 4 b] +*[a b] *[a 0 b] /[b a] *[a 1 b] b
In English, this says “when we have subject a,
function 4, and
Nock code b, first evaluate [a b]
as
[subject formula],
and then add 1 to the result.”
If we contrast with 0 and 1, we see that the
right side has
a * symbol. This symbol means “evaluate the
expression
again in the Nock interpreter.” 0 and 1 did not have this
symbol, and that’s why they couldn’t evaluate nested Nock
expressions.
Let’s start by translating the Dojo’s .*(subject formula)
to pseudocode of the form *[a b],
and then expand it line by
line:
> .*(50 [4 0 1]) 51 :: change to pseudocode *[50 [4 0 1]] 5:: move the 4 to the outside as + +*[50 [0 1]] :: expand the 0 opcode to the memory slot operator "/" +/[1 50] :: grabs the memory slot 10+(50) :: evaluate 51
The [a b]
part of +*[a b]
expands to:
[50 [0 1]]
OK, this we know how to handle! It’s just our 0 function, and
it wants the value in memory slot 1 of the
subject. That’s
50.
Now we know that *[a b]=50,
and we just have to add 1
to it (the + in +*[a b]).
That is 51, which is exactly what
the interpreter gave us.
This one is similar, we just have an extra 4. We again start
by translating the Dojo’s .*(subject formula)
to
pseudocode, and then expand
> .*(50 [4 4 0 1]) 52 *[50 [4 4 0 1]] :: the first 4 moves outside as a '+' 5+*[50 [4 0 1]] :: 2nd 4 becomes a '+'...we have opcode 0 again! ++*[50 [0 1]] ++/[1 50] ++(50) 10+(51) 52
Here we again see lots of 4s applied
consecutively, and we also
see how we can yank values out of a more complicated subject
and manipulate them. Notice how the subject is a cell,
not an atom. The rest is the same as in the previous
example.
> .*([100 150] [4 4 0 3]) 152 a (the subject) = [100 150] *[[100 150] [4 4 0 3]] 5+*[[100 150] [4 0 3]] :: Now we've extracted all the increments, :: so we just grab the value at memory slot 3 ++*[[100 150] [0 3]] ++/[3 [100 150]] 10++(150) +(151) 152
In the below example, we see how we can use the quote/constant
function 1 to
generate the value 98 and increment it. We
ignore the subject 50 completely.
> .*(50 [4 1 98]) 99 *[50 [4 1 98]] :: formula is the "quoter" function 5+*[50 [1 98]] +(98) 99
Just as opcode 0 had values it
couldn’t handle (non-atoms), so
opcode 4 needs
the nested value inside it to evaluate to an
atom.
> .*(50 [4 1 [0 2]]) dojo: hoon expression failed *[50 [4 1 [0 2]]] :: OK cool, the nested value is a 1 opcode 5+*[50 [1 [0 2]]] :: 1 ignores the subject (50) and just returns [0 2] +([0 2]) :: [0 2] isn't an atom, so how can we increment it??? :: We can't, so we crash. 10dojo: hoon expression failed
4In these examples, we’ve seen that function 4 can be called as
many times in a row as we want. At the end of those calls, it
always ends up incrementing a number that either is yanked
from the subject (memory slot function 0) or quoted as it
is
(quote function 1).
The Nock interpreter is allowed to return nouns, which are atoms (positive numbers) or cells (pairs of nouns). What have our functions/opcodes been returning so far?
0: atoms or
cells, depending what’s in the memory
slot that we yoink.
1: atoms or
cells, depending on what we quote.
4: just atoms.
But what if my subject was [51 67 89],
and I wanted to
increment every value and return that as [52 68 90]?
How
can I do that when it’s a cell, and 4 only seems able to
return
atoms?
The answer is something that the Nock docs call the “distribution rule” or “implicit cons” (hello, fellow lispers!), but that I find easiest to think of as the “Cell-Maker Rule”.
We haven’t talked much yet about what values are legal to
feed into the Nock interpreter (the .*(subject formula)
function in the Dojo). So far, we’ve only been using formulas
that start with numbers (our functions/opcodes 0/1/4).
Let’s now fully solidify our understanding of what’s a legal
formula by taking a quick look at the three possible cases.
(The format is.*(subject formula).)
The formula is a cell starting with an opcode. We know this is OK.
> .*(50 [0 1]) 50
The formula is just an atom (0). This is not valid.
> .*(50 0) dojo: hoon expression failed
Finally, we try a formula that is a cell starting with an atom. This looks invalid, but—it works!
> .*(50 [[0 1] [1 203]]) [50 203]
So apparently a formula cell can start with a cell. The Cell-Maker rule is:
*[subject [formula-x formula-y]]→ [*[subject formula-x] *[subject formula-y]]
In our example above, formula-x
is [0 1],
and
formula-y is [1 203].
They each evaluate individually
against the subject, and the end result is a cell.
We can make as many cells in a row as we want:
> .*(50 [[0 1] [1 203] [0 1] [1 19] [1 76]]) [50 203 50 19 76]
We can put any operation inside each cell:
> .*([19 20] [[0 1] [1 76] [4 4 0 3]]) [[19 20] 76 22]
If we take the returned collection [[19 20] 76 22]
in
order, we can write in English how they connect to our
collection of formulas that we passed:
[0 1]:
get memory slot 1
[1 76]:
return the quoted value 76
[4 4 0 3]:
increment twice the value in memory
slot 3 (20)
So we can pass one small subject ([19 20])
and make an
arbitrarily long collection of values from it, using any
functions we want. Cell-Maker ftw!
3, the Cell
Detector, and 5,
the Equality TesterNow we come to functions/opcodes 3 and 5, which are pretty
straightforward after we’ve seen how 4 and the Cell-Maker
work. Functions 3
and 5, like 4, allow nested
evaluation.
Let’s put all their pseudocode definitions together to
compare:
:: function/opcode 3 *[a 3 b] ?*[a b] :: function/opcode 4 *[a 4 b] +*[a b] 5:: function/opcode 5 *[a 5 b c] =[*[a b] *[a c]]
First of all, notice how the right side of all these “equations”
has the evaluation operator, *. This means that
these
functions can have nested formulas, since they keep evaluating
all the way down.
There are some new pseudocode symbols here that we need
to translate into English. We already know +:
“increment the
value after this". Now we also see:
?: “check whether the
value after this is a cell. Return
0 if yes, 1 if no".4
=: “first run the function
in b with subject a as the
argument, and same for the function in c.
If the
results are equal, return 0, if not, return 1.
> .*(50 [3 0 1]) 1 :: PSEUDOCODE OF THE ABOVE *[50 [3 0 1]] 5?*[50 [0 1]] ::get memory slot 1 of the subject ?(50) :: is 50 a cell? No, so return 1 1
> .*([50 51] [3 0 1]) 0 :: PSEUDOCODE OF THE ABOVE *[[50 51] [3 0 1]] 5?*[[50 51] [0 1]] ::get memory slot 1 of the subject: [50 51] ?([50 51]) :: is [50 51] a cell? Yes, so return 0 0
4
> .*([50 51] [4 4 3 0 1]) 2 :: PSEUDOCODE OF THE ABOVE *[[50 51] [4 4 3 0 1]] 5+*[[50 51] [4 3 0 1]] :: whatever comes out of the 3 function, :: we're gonna increment it twice ++*[[50 51] [3 0 1]] :: down to just fetching memory slot 1 10++?*[[50 51] [0 1]] ++?([50 51]) :: is [50 51] a cell? Yes, so return 0 ++(0) +(1) 152
> .*([[50 51] 52] [[3 0 2] [3 0 3]]) [0 1] *[[[50 51] 52] [[3 0 2] [3 0 3]]] ?[*[[50 51] 52] [0 2]] 5 *[[50 51] [0 3]]] :: yank memory slots 2 and 3 ?*[[50 51] 52] :: first is a cell, second is not [0 1]
Because 5 compares the
results of 2 formulas, it always makes
2 inner evaluations of the subject. It’s similar to Cell-Maker in
this way.
> .*([50 51] [5 [0 2] [0 2]]) 0 :: PSEUDOCODE *[[50 51] [5 [0 2] [0 2]]] 5:: factor out the = =[*[[50 51] [0 2]] *[[50 51] [0 2]]] :: get memory slot 2 twice =(50 50) 0
> .*([50 51] [5 [0 2] [0 3]]) 1 :: PSEUDOCODE *[[50 51] [5 [0 2] [0 3]]] 5:: factor out the = =[*[[50 51] [0 2]] *[[50 51] [0 3]]] :: get memory slot 2 and memory slot 3 =(50 51) 1
> .*([50 51] [5 [4 0 2] [0 3]]) 0 :: PSEUDOCODE *[[50 51] [5 [4 0 2] [0 3]]] 5:: factor out the = =[*[[50 51] [4 0 2]] *[[50 51] [0 3]]] :: factor out the + =[+*[[50 51] [0 2]] 10 *[[50 51] [0 3]]] :: get memory slots 2 and 3 =[+50 51] :: evaluate the + =([51 51]) 150
> .*([99 99] [5 [1 [99 99]] [0 1]]) 0 :: PSEUDOCODE *[[99 99] [5 [1 [99 99]] [0 1]]] 5=[*[[99 99] [1 [99 99]]] *[[99 99] [0 1]]] :: first cell is the result of quoter function :: second cell is the result of memory fetch =[[99 99] [99 99]] 10:: true 0
3 and 5These along with 4 are known as the
“axiomatic” functions.
They exist to implement definitional logic for the Nock
specification. In particular, the cell check and the equality
check provide for structural analysis of nouns.
2, the
“Subject-Altering” FunctionIn all our examples so far, the subject has been defined at the start when we call the interpreter, and never changes. But what if we want to change the subject?
A different subject? Why would we want that? Here’s an easy example. Say you found the following piece of Nock code on the interwebz:
[8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1]
This is the code for a Nock function that expects a subject that is an atom, and decrements that subject by 1. You can actually enter it in the Dojo right now:
> .*(100 [8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1]) 99
This works! You do not have to understand the code right
now; just try entering different numbers instead of 100 to see
the program working.
But now imagine that I have a Nock program with a different subject
> .*([50 51] some-formula)
And somewhere inside some-formula, I want to
decrement the number 51. I can’t pass [50 51]
as the
subject to my decrementer code above though, because that’s
a cell, and it expects just an atom (a number).
The function/opcode 2 is designed to
handle this problem for
us. First the pseudocode:
*[a 2 b c] *[*[a b] *[a c]]
2
expects 2 formulas after the subject a: b and c. With
those, it:
runs formula b against
the subject to set up a new
environment/subject derived from the subject
runs formula c against
the subject to prepare a 2nd
function
run that 2nd function against the new environment/subject from step (1)
Note that the pseudocode for 2 has nested *s.
*[*[a b] *[a c]]
The two inner *s run steps (1)
and (2), and the outer one,
around the whole expression, runs step (3).
> .*([50 51] [2 [0 3] [1 [4 0 1]]]) 52 :: PSEUDOCODE *[[50 51] [2 [0 3] [1 [4 0 1]]]] 5:: separate b and c to each run against the subject (steps 1 and 2) *[*[[50 51] [0 3]] *[[50 51] [1 [4 0 1]]]] :: after steps 1 and 2, we have a new subject, 51! :: note how we're back in normal *[subject formula] form *[51 [4 0 1]] 10:: apply the 4 function as we're used to +*[51 [0 1]] :: grab 51 from memory slot 1 +(51) 52
Think of this as grabbing a “stored procedure” from the subject.
> .*([[4 0 1] 51] [2 [0 3] [0 2]]]) 52 :: PSEUDOCODE, subject is [[4 0 1] 51] *[[[4 0 1] 51] [2 [0 3] [0 2]]] 5*[*[[[4 0 1] 51] [0 3] *[[[4 0 1] 51] [0 2]]]] :: step 1 gets memory slot 3, step 2 grabs memory slot 2 *[51 [4 0 1]] :: looks like a normal 4 opcode to me! 10+*[51 [0 1]] :: grab memory slot 1 +(51) 52
Remember our decrementing block of code that we couldn’t
use when the subject was [50 51],
instead of just an
atom? Opcode 2
makes handling that issue a piece of
cake.
We simply use 2 to transform our
subject into an atom,
and use 1 to
quote the decrement block of code before it
evaluates in step (3).
> .*([50 51] [2 [0 2] [1 [8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1]]]) 49 :: PSEUDOCODE (subject is [50 51]) :: ("decrement-formula" substituted for clarity) 5*[[50 51] [2 [0 2] [1 decrement-formula]]] *[*[[50 51] [0 2]] *[[50 51] [1 decrement-formula]]] *[50 decrement-formula] ::decrement-formula has the atom subject that it wants 49
2For those who know a bit of Hoon, the second example above
is rather similar to calling an arm that produces a gate, and
then running the gate. Most of Hoon runs this type of
stored-procedure plus subject-altering Nock, and it all uses
opcode 2 at its
base.
And for those who know Hoon, [[4 0 1] 51]
should
already be looking a lot like [battery payload]…
that’s
not a coincidence. We’re starting to see the first glimpses of
how Hoon’s cores, arms and subjects/subject mutations flow
out of the fundamental structure of Nock.
We also see how Hoon/Nock lend themselves well to throwing around chunks of code, and adjusting the subject as necessary to create the correct subject/environment against which to run that code.
You now have seen all the fundamental functions/opcodes in
Nock. In the next part, I’ll introduce the remaining functions,
which no longer need pseudocode: we have enough scaffolding
now to build the rest of Nock from Nock itself. Instead, these
new opcodes will just be shortcuts/macros/code expansions
building on opcodes 0–5.
We’ll also start to connect Nock to Hoon, and see how most of the fundamental (and slightly weird) features of Hoon flow directly from Nock’s structure, and make a lot more sense in combination with it.
A word of encouragement: we’re done with the hard part now. Every Nock function we learn in this section will be built from pieces in the preceding section.
None of these new functions are necessary to make Nock
work. All of them except Nock 10 and 11 are syntactic
sugar
that is part of the Nock definition, and must be built into
every correct Nock implementation. If you have seen macros or
code expansions in other languages, that’s another word for
what’s happening here.
Nock 10 makes it easier
to replace a memory value
somewhere in a tree, and Nock 11 allows passing
hints to the
interpreter.
One point of clarity: this syntactic sugar/code-expansion system is not extensible. This means that you can’t invent your own Nock opcodes and still have that language be Nock; you’re making a higher-level language on top of Nock at that point.
In fact, that’s not a bad way to think of Hoon: it’s a higher-level language that adds missing syntatic sugar/macros and human-readable names to Nock. (That’s not the whole story, but it’s a decent mental peg to initially hang Hoon on.)
Nock is intentionally very, very small, such that you can always walk through and analyze what is happening in a block of code if you know Nock’s opcodes.
1 (Quoter Function)
You’re going to see the 1 opcode (the
“Quoter”) appear in a
lot of examples below for a simple reason: the 6-9 opcodes
expect formulas in a lot of places, not just atoms. And, as
we’ve seen already, formulas have to be cells.
Whenever a formula is required, but you really just want to return a number, you use the quoter function.
:: We just want to run 4 on the number 5, :: but 4 expects a formula after it, so we use [1 5] > .*(0 [4 1 5]) 6
:: we grab memory slot 2 :: then it has to be compared to the result of a formula :: so we just use the formula [1 23] to return 23 > .*([23 45] [5 [0 2] [1 23]]) 50
6, “If/Else”
Conditional BranchThe remaining Nock opcodes are “sugar”. This means that the
functions in this next part will use only * and
Nock code in
their pseudocode. For example, here is the code for 6, the
“If/Else" function.
*[a 6 b c d] *[a *[[c d] 0 *[[2 3] 0 *[a 4 4 b]]]]
The prose explanation of what’s happening is straightforward:
Evaluate b against the
subject a (*[a b])
to see
whether it’s 0/true or 1/false.
If b equals 0/true, run formula c against subject a.
If b equals 1/false, run formula d against subject a.
If b is not equal to
0 or 1, the code crashes, for
reasons we’ll see in the code explanation.
OK, so that’s the English version. The code explanation (the right side of the definition) is really fun now that we know the basic Nock opcodes.
The pseudocode has four nested *[subject formula]s,
so I’m going to unwrap those to the bottom, and then build it
up again. The layers are, in order:
*[a ...],
i.e. subject a evaluated against that long
formula starting with *[[c d] 0 ...].
*[c d],
i.e. subject c evaluated against the
formula
starting with [[2 3 ...].
*[2 3],
i.e. subject 2 evaluated against the
lowest-level formula.
Finally, subject a
evaluated against formula
[4 4 b].
Remember, our English explanation was “see if *[a b]
is
true or false, and do different actions depending on that. Step
Four is that check.
Let’s say we have a as 59, and b as the quoted value
0/true.
*[a 4 4 b] :: a: 59 :: b: [1 0] *[59 4 4 [1 0]] 5:: substitute out the two increment operators ++*[59 [1 0]] :: ignore subject, return quoted value 0 ++(0) 2
In summary, because *[a b]
evaluated to 0/true, we get
the number 2. If *[a b]
had been 1/false,
we’d get 3
(because we’d evaluate ++(1)).
What the heck? Why are we getting 2 or 3 back? How
does that help us?? Well, Nock uses that returned 2 or 3 as
a memory slot, and executes the code in that memory
slot.
Now we go up to step 3, with the subject [2 3]
evaluated
against our return value from step 4. Let’s imagine that 2 had
been returned:
:: remember, "result-of-step-4" was 2 *[[2 3] 0 result-of-step-4] *[[2 3] 0 2] :: get memory slot 2 52
This grabs memory slot 2 if
*[a b]
was true, and
memory slot 3 if *[a b]
was false.
Wait, isn’t this redundant? We are just using our 2
or 3 generated in step 4 to generate a 2 or a 3. Seems
dumb.
The answer is that we make sure that a crash happens if
*[a b]
yields any answer other than 0/true or 1/false. If
*[a b]
returned 10, for example, we’d have the
following
code in step 3:
*[[2 3] 0 10] :: there's no slot 10 CRASH!!
This is exactly what we want: the program crashes unless we are doing
a loobean5
test that returns a 0 or 1 (converted to an indicial 2 or 3) in
step 4.
We now have our validated 2 or
3 to plug into step 2.
Let’s imagine c is the simple formula [0 1]
and d is
[1 203].
:: if step 3 returned "2" (true) *[[[0 1] [1 203]] 0 2] [0 1]
Not much to see here: we just grab memory slot 2 or 3
depending on whether our initial b was true or
false.
And now we’re back at the top level, where we just use
whichever formula we yoinked in step 2 and run it against
a.
*[a formula-from-step-2] :: let's say we returned formula [0 1] :: our original a, from step 4, was 59 *[59 [0 1]] 559
6> .*(1 [6 [0 1] [0 1] [4 0 1]]) :: PSEUDOCODE :: *[a *[[c d] 0 *[[2 3] 0 *[a 4 4 b]]]] *[1 *[[[0 1] [4 0 1]] 0 *[[2 3] 0 *[1 4 4 [0 1]]]]] 5:: factor out the 4 opcodes *[1 *[[[0 1] [4 0 1]] 0 *[[2 3] 0 ++*[1 [0 1]]]]] :: b evaluates to 1 (yank memory slot 1) *[1 *[[[0 1] [4 0 1]] 0 *[[2 3] 0 ++(1)]]] :: evaluate the two increments 10*[1 *[[[0 1] [4 0 1]] 0 *[[2 3] 0 3]]] :: get memory slot 3 from [2 3] *[1 *[[[0 1] [4 0 1]] 0 3]] :: [0 3] means get memory slot 3 from the subject (formula [4 0 1]) *[1 [4 0 1]] 15:: factor out the 4 opcode +*[1 [0 1]] +(1) 2
6Now I’m going to make you a little sad. Most Nock interpreters
don’t do this whole awesome code expansion. They just see 6,
and implement an if/else check with a crash if *[a b]
isn’t a
loobean.
However, the pattern of storing chunks of code in memory and pulling them out when you want them is the most important part of Nock. In fact, those of you who know Hoon are probably already seeing the makings of the “core” code pattern.
7, the “Composition”
Opcode7 is so simple we
barely need to spend time on it. All it does is
create a new subject/environment (using 2), and immediately
runs a formula against that new subject. Let’s compare it to
2:
::opcode 7 *[a 7 b c] *[*[a b] c] :: opcode 2 5*[a 2 b c] *[*[a b] *[a c]]
This is almost exactly the same except with c instead of
*[a c].
This means that you can write a “subject-changing"
formula in b, and then run a simple function
against that in
c.
2 vs. Opcode 7:: using opcode 2 > .*([23 45] [2 [0 3] [1 4 0 1]]) 46 5:: using opcode 7 -- we get to remove the quoter opcode "1" :: wow amazing /sarcasm > .*([23 45] [7 [0 3] [4 0 1]]) 46
Opcode 7 is clearly
trivial, so why does it exist? It allows
clean expression of function composition: this is really
c(b(a)),
where a (the subject) is the initial argument,
and b
and c are functions. This pattern comes up a
ton, and it’s nice
to not use 1s
everywhere.
8, the “Variable
Push” OpcodeIf you’re ever writing Nock and think “how can I add a new
variable to the subject?", opcode 8 is what you want.
The new
variable can be based on either the existing subject, or be a
new value you add on.
*[a 8 b c] *[[*[a b] a] c]
This says to run *[a b],
and then make that the head of
a new subject, with the old subject a as the new
subject’s
tail.
In English, the below code first yanks the variable from memory slot 3, copies it to the head of a new subject, and then increments the value in that new head.
> .*([67 39] [8 [0 3] [4 0 2]]) 40 :: PSEUDOCODE *[[*[[67 39] [0 3]] [67 39]] [4 0 2]] 5:: yanks mem slot 3 and pins it to the front of the old subject *[[39 [67 39]] [4 0 2]] +*[[39 [67 39]] [0 2]] +(39) 40
> .*([67 39] [8 [1 0] [4 0 2]]) 1 :: PSEUDOCODE *[[*[[67 39] [1 0]] [67 39]] [4 0 2]] 5*[[0 [67 39]] [4 0 2]] +*[[0 [67 39]] [0 2]] +(0) 1
Why do we want this? In the first example, we pin a copy of a
value so that we can manipulate it without changing the
original. In the second example, we add a 0 to the front;
maybe we want to increment it until some condition is
met?
The above should be starting to feel very Hoon-ish: we’re a minor code transform away from pinning new values to the head of a payload.
9, Run a Stored
Procedure Arm in a CoreWe’re almost at full Hoon now, although still at a very
low/raw level. 9
looks a little complicated...
*[a 9 b c] *[*[a c] 2 [0 1] 0 b]
... but in English, this is just saying:
Use formula c to make a
new subject from a
(*[a c]).
Grab the formula located at memory slot b in that
new subject.
Run that formula against the new subject *[a c].
The fact that the above description has the words “make a
new subject" tells us right away that it’s syntactic sugar for
opcode 2, and
that’s indeed what we see in the pseudocode.
9 to Run an
Increment ArmThe initial expression here likely looks cryptic, but if you follow the pseudocode, it will become clear.
To stay oriented, remember that, if we’re thinking of 9 as
*[a 9 b c],
then
a: 45 b: 2 c: [[1 4 0 3] 0 1]
> .*(45 [9 2 [1 4 0 3] 0 1]) 46 :: PSEUDOCODE *[45 [9 2 [1 4 0 3] [0 1]]] 5*[*[45 [1 4 0 3] [0 1]] 2 [0 1] 0 2] :: new subject is [[4 0 3] 45] :: that is a formula to increment mem slot 3 in the :: head; 45 in the tail *[[[4 0 3] 45] 2 [0 1] 0 2] 10:: now we expand opcode 2 *[*[[[4 0 3] 45] 0 1] *[[[4 0 3] 45] 0 2]] :: mem slot 2 of the subject becomes the new formula *[[[4 0 3] 45] 4 0 3] 15+*[[[4 0 3] 45] 0 3] :: grab mem slot 3 +(45) 46
We start above with a subject that is not a core; it’s just
the atom 45. The code for c is then:
[[1 4 0 3] [0 1]]
This formula uses the Cell Maker (Distribution Rule) to
insert [4 0 3]
as the head of the new subject, and puts mem
slot 1 of the old subject as the tail, so we get
a new subject of
[[4 0 3] 45].
What we do next is use b (here,
2) to select memory slot 2
from that new subject. Memory slot 2 is a
formula: [4 0 3].
We run that formula against the new subject.
When I first saw 9, I thought: “why
didn’t they just use 2 to
make the transformed subject? Why is there an extra step to
use [0 1]
to pull the new *[a c]
subject? Why can’t we do
*[a 2 c [0 b]]?
The answer is that we actually use the *[a c]
subject
twice:
We extract from it the formula located at memory
slot b.
Then we run that formula against the *[a c]
subject.
If we just did *[a 2 c [0 b]],
then [0 b]
would try
to look up the b memory slot in a, not *[a c].
So 9 gives us
one extra step to set up the core itself.
9I like to think of 9 as having three
parts:
c: our formula to set up
the subject, making a new
subject.
b: the memory slot in our
new subject where an arm
is.
Run the arm located at b
against the new subject.
You can think of this as setting up a subject, pulling a stored procedure from it, and then running that procedure against the subject.
10, Replace a Memory
SlotBefore explaining 10, we need to
introduce a new operator, #
hax. # hax is the “edit" operator. It has
the form
#[mem-slot new-val target-tree]
It replaces the memory slot mem-slot in target-tree with
new-val.
:: Example #[2 [4 5] [99 88 77]] [[4 5] 88 77]
The pseudocode for 10 is:
*[a 10 [b c] d] #[b *[a c] *[a d]]
In English, this first calculates *[a c]
and *[a d],
and
then replaces memory slot b in the latter with
the result of the
former.
10 to Replace a
Memory
Slot> .*(50 [10 [2 [0 1]] [1 8 9 10]]) [50 9 10] :: PSEUDOCODE *[50 [10 [2 [0 1]] [1 8 9 10]]] 5#[2 *[50 0 1] *[50 1 8 9 10]] #[2 /[1 50] [8 9 10]] #[2 50 [8 9 10]] :: expanded as far as we can, now do the edit :: replace mem slot 2 of [8 9 10] with the value 50 10[50 9 10]
We will defer discussion of opcode 11 to a later
section
because it is not part of strict Nock semantics.
If “grab a chunk of code from a subject and then run it
against the subject" sounds a lot like getting an arm from
a core in Hoon, that’s because it is. Nock opcode 9 is
hand-in-glove with Hoon’s core/arm structure. The “new
subjects" created by *[a c]
are cores, and the things selected
from memory slots by b are arms.
To finish this off and take your new powers for a spin, let’s
look at some real Nock code from the wild. I got the below
example from the Dojo. It’s a mold: a function that takes a
noun and returns it if it’s the correct type, and crashes if not.
The mold here checks whether the input noun is a loobean
(0/true or 1/false).
:: loobean mold gate > =loobean-mold ? :: below output truncated for our purposes here 5> loobean-mold < 1.fxf ... > :: grab the code for the battery > -.loobean-mold 10[8 [6 [5 [1 0] 0 6] [1 0] 6 [5 [1 1] 0 6] [1 1] 0 0] 8 [5 [0 14] 0 2] 0 6]
So we:
Assign the mold gate denoted by ? to the face
loobean-mold.
Examine what’s inside, seeing that the head is an arm.
Print out that source code by calling the head.
The below code acts as a formula which evaluates its sample, and returns it if it’s a loobean or crashes otherwise. Let’s see how that works.
[6 [5 [1 0] 0 6] [1 0] 6 [5 [1 1] 0 6] [1 1] 0 0]
We start with 6, which means this
is an if-else. The true/false
test is the next element:
[5 [1 0] 0 6]
This compares the quoted value 0 (from [1 0])
with the
value at memory slot 6 in the subject ([0 6]).
What is the subject and what is at mem slot 6? This code
is the arm of a gate, so the subject is that gate/core:
[battery [sample payload]].
We are looking at the
battery right now, and so [0 6]
yanks the head of the tail, or
the sample!
We know the sample will be a noun that we’re testing for
loobeanness, so this code starts by seeing whether the sample
is the value 0/true. If it is, the next element
is [1 0],
so we
return 0 if the sample is 0.
Otherwise, we run the second branch of the if–else
conditional:
[6 [5 [1 1] 0 6] [1 1] 0 0]
This is also an opcode 6 if-else. Once
again, it compares
something to the value at mem slot 6 (the
sample), but this
time it checks whether that is the value 1. If
it is, it runs the
formula [1 1]
to return 1.
If not, it means our input was neither 0 nor 1
and is not a loobean, so we run the formula [0 0],
which always crashes (as there is no memory slot
0).6
This is exactly what we want—crash if the sample is not a
loobean!
The second part of the formula which is composed with an
8 is:
[8 [5 [0 14] 0 2] 0 6]
This checks whether the battery of the current gate is equivalent to the head of the context; if so, it returns the sample. This is a artifact of a type promotion in Hoon which converts a bare loobean value to a constant by pinning a constant as an example first (i.e., at slot 14). (It’s completely extraneous in Nock itself, however.)
In this section, we’ve seen how to use almost all of the
remaining opcodes, which build Nock up to a slightly more
expressive level. We also saw how Hoon cores start to arise
pretty naturally out of the Nock primitives, especially 8 and
9. Then we walked
through real production Nock code to show
that everything we’ve learned so far works exactly as expected
in the wild. In the next section, you’ll learn how to write real
programs in Nock, and compose those programs to make new
ones. Finally, hopefully you now see that, whatever its other
limitations, Nock is not particularly obscurantist, and is fairly
straightforward to parse, once you understand its syntax and
idioms.
In this section, we cover some loose ends deriving from the previous discussion.
At this point, we can answer the question of what order Nock evaluates expressions in. The answer is straightforward: it starts with code that has only one pseudocode operator and all Nock code, as below:
*[50 4 4 [5 [0 1] [1 50]]]
The interpreter can then be thought of as moving left-to-right, expanding according to its rules, until it can’t expand any further into pseudocode:
*[50 4 4 [5 [0 1] [1 50]]] +*[50 4 [5 [0 1] [1 50]]] ++*[50 5 [0 1] [1 50]] ++=[*[50 [0 1]] *[50 [1 50]]] 5++=[/[1 50] 50]
Once we get to that last line, ++=[/[1 50] *[50 [1 50]]],
no further expansion into pseudocode is possible.
At this point, the interpreter expands “inside-out", starting
from the deepest operators. In this case, those are /[1 50]
and 50, so it does those:
++=[50 50]
Then it moves to the next-furthest-inside operator: =, and
then to the + operators:
++=[50 50] ++(0) +(1) 2
On the first pass, when we have
Nock code *(nock-code),
we expand left-to-right
into pseudocode.
On the second pass, when we’ve fully expanded pseudocode, we evaluate operators from the inside-out.
11, Hints and Side
Effects for the InterpreterOpcode 11 lets you compute
side effects and pass information
to Nock’s interpreter, for that interpreter to do what it wants.
The most common uses are things like jets and debugging
prints. In theory, this opcode is fairly dangerous, since it tells
the interpreter that it’s free to do anything.
There are two different versions of 11, depending on
whether the head following 11 is an atom or a
cell
:: head is an atom (b) *[a 11 b c] *[a c] :: head is a cell ([b c]) 5*[a 11 [b c] d] *[[*[a c] *[a d]] 0 3]
This pseudocode lets 11 handle two
separate use
cases:
We just want the interpreter to process a message in its own language/environment.
We want the interpreter to compute some Nock code with Nock semantics before processing the hint.
Imagine the following Nock:
.*([50 51] [11 369 0 2])
This passes the value 369 to
the interpreter, where maybe it
would be the key in a hashmap. The value associated with the
could be the function to debug print the whole operation. Or
the value could be a jet function that specifically knows how
to compute the 0
opcode faster when it’s followed by a
2.
After the interpreter does whatever, it needs to then
discard the value 292.989, and
computes
> .*([50 51] [0 2]) 50
In this case, instead of passing a static value to the interpreter, we pass it a Nock computation against the subject. The result of that computation will then be available to the interpreter to use as a message.
11: Jet Registration
Jet registration in Hoon usually looks like this:
++ my-function ~/ %my-function |= var=* ...
The Hoon rune ~/ fassig uses
Nock 11 to pass
the value
%my-function to the interpreter, where it is
associated with
the C code that produces the product of my-function.
In Hoon, you can acquire the Nock code for any function by
using the != zaptis rune. Since this produces
Nock code
complete with gate calls, you may also find it helpful to cast a
data type as a noun using ^- *,
which will show you the
raw Nock code for that value.
As you have seen, you can also evaluate raw Nock using
the .* dottar rune, which evaluates to Nock
opcode 2. Other
Nock runes in Hoon include .+ dotlus, which is
opcode 4; .=
dottis, which is opcode 5; and .? dotwut, which is opcode 3.
Fake opcode 12 is
not actually Nock, but is used in a
virtualization context to resolve values that may not be
available in the current subject.
At this point, you now know everything there is to know about Nock syntax and basic code manipulation. However, if I asked you to go write a simple program in Nock, you’d probably have a hard time getting started. It’s really helpful to see some examples of how Nock programs are designed and patterns that tend to recur in them.
We can set variables to formulas in the Urbit Dojo. We will use that in this lesson to make code easy to follow, and to show how Nock programs are made out of discrete chunks.
> =increment-formula [4 0 1] > .*(50 increment-formula) 51 > =increment-formula
Every Nock program is just a formula that takes in a subject (argument). In order to run full programs against a subject, we follow the following pattern:
First pass: set up the dominos inside an opcode like
2 (or 7/8/9). This will
create a core, and evaluate it
on the second pass.
Second pass: evaluate that core to get our result.
The pseudocode for opcode 2, this looks like:
*[subject 2 core-formula call-formula]
Almost always, however, we’ll use the 9 opcode (which is
sugar on top of 2) to actually start
our programs running,
since it supports the concept of “cores" and “arms" very
naturally. (For those who know Hoon, this “set up a
core and run it” pattern should feel similar to |^ or
=>.)
Let’s take code to increment the subject and turn it into a
Hoon-style gate (a core with one arm and a sample). The code
itself is simple: [4 0 1].
Our code expects the subject to be an atom, but Hoon
gates expect their subject to be the gate itself, which has the
form [battery payload].
So we need to adjust our
formula to accept this subject format.
> =inc [7 [0 3] [4 0 1]] :: verify that it increments value in the subject's tail (payload) > .*([1 74] inc) 75
We put our formula in the head, and put a default
(“bunted”) sample of 0 as the payload.
> =inc-gate [inc 0] > inc-gate [[7 [0 3] 4 0 1] 0]
Arms are best invoked using the 9 opcode. Here we
use the
“standard" version of it: [9 2 0 1].
Recall that 9 is
*[a 9 b c],
where c is the “new subject" formula, and
b
is the memory slot of that new subject to take an arm
from. Here we use [0 1]
to keep our subject (the gate)
unchanged.
> .*(inc-gate [9 2 0 1]) 1
To “pass a parameter" to our gate, we use the 10
opcode to edit the subject (the inc-gate core)
and
replace the payload with a value. We make our subject
[inc-gate val-to-increment]:
:: notice how opcode 10 can replace the last element of inc-gate :: the tail of inc-gate was 0; now it's 36 > .*([inc-gate 36] [10 [3 [0 3]] 0 2]) [[7 [0 3] 4 0 1] 36] 5 :: now use that to set up the subject with a new tail (sample) :: and call arm in memory slot 2 (our increment formula) > .*([inc-gate 36] [9 2 10 [3 [0 3]] 0 2]) 37 10> .*([inc-gate 562] [9 2 10 [3 [0 3]] 0 2]) 563
What was the point of this? We took a perfectly good increment formula that worked on atoms, and made it more complicated for the same result. Lame!
In fact, however, this setup will come in really handy when we have multiple arms in our core, not just one. We’ve made it easy to set up a clean environment for increment to find its sample in, no matter what other data is present. This will come in very handy in our third example program.
First, however, let’s look at putting a more complicated formula inside a gate. (Hint: the process is the same).
Here we take a piece of code that decrements the subject when
the subject is an atom, and turn it into a gate. For now, we
will take it as a given that the decrement function given below
works. (The code will crash when the input is a cell or
0)
:: the code: set a Dojo face =dec > =dec [6 [5 [0 1] [1 0]] [0 0] [6 [3 0 1] [0 0] [8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1]]] :: testing in the Dojo 5> .*(100 dec) 99 :: with non-atom input we crash .*([100 101] dec) 10dojo: hoon expression failed
Let’s re-jigger the decrement formula to accept the subject
in format [battery payload]:
:: gets value in mem slot 3 and applies the decrement formula to it > =dec-arm [7 [0 3] dec] :: verify that dec-arm decrements the value in the tail 5> .*([1 88] dec-arm) 87 :: output the full dec-arm formula code > dec-arm 10[7 [0 3] 6 [5 [0 1] 1 0] [0 0] 6 [3 0 1] [0 0] 8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1]
Next, assemble the core:
:: all we need to do is add the sample! (we give it a default value of 0) > =dec-gate [dec-arm 0] > dec-gate [[7 [0 3] 6 [5 [0 1] 1 0] [0 0] 6 [3 0 1] [0 0] 8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1] 0] 5[[7 [0 3] 6 [5 [0 1] 1 0] [0 0] 6 [3 0 1] [0 0] 8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1] 0]
As in the first example, we use the 10 opcode to edit
the
subject (the dec-gate core) and replace the
payload with a
value. We make our subject [dec-gate val-to-decrement].
:: confirm that our 10 code places 36 in the tail > .*([dec-gate 36] [10 [3 [0 3]] 0 2]) [[7 [0 3] 6 [5 [0 1] 1 0] [0 0] 6 [3 0 1] [0 0] 8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1] 36] 5:: now use that to set up the subject with a new :: tail (sample) and call arm in memory slot 2 :: (our decrement formula) > .*([dec-gate 36] [9 2 10 [3 [0 3]] 0 2]) 35 10> .*([dec-gate 562] [9 2 10 [3 [0 3]] 0 2]) 561
In this example we will build a Nock core that compares two numbers and returns whether they are greater than, less than, or equal to each other.
The program specification is to take two numbers a and b
and return:
0 if a==b.
1 if a>b.
2 if a<b.
The trick is that the only mathematical operators we have
for this are the 4 opcode for
increment, 5 for
equals, and a
decrement Nock function that we will supply. The basic
algorithm is:
If a==b, return 0.
If a==0, return 2. (I.e, a<b).
If b==0, return 1. (I.e., a>b).
Recur with a and b both decremented.
The above works because if a is
smaller than b, it hits 0
first. If b is smaller than a, it hits 0 first. If they are equal, we
never decrement in the first place, so there are no issues with
numbers going negative.
We will construct a core that has two arms: one arm with the algorithm logic, and a second arm with the decrement gate from the second example. These arms will live in the head of the core (think “battery").
We will put our variables a and
b in the tail of the core
(think “payload"). They will be updated before the core is
called each time. (This is similar to a trap or door in
Hoon).
The final core we will create will have the structure
[battery payload],
which can be broken down as:
[[main-logic dec-gate] a b]
Once the core is set up, we’ll invoke the algorithm logic arm to set it running. We will build the main logic “inside-out", by first defining the “recur" code, and then inserting it into our if/else tests that implement the algorithm.
This recursion logic assumes the decrement gate lives in
the tail of the battery (the battery is the head), i.e. [0 5].
We are using [10 [3 [0 memory-slot]] 0 5]
to extract
the decrement gate from our core, and then we invoke it with
[9 2 ...].
This is identical to what we did in the second example—the
only difference is that we now do it twice: once for memory
slot 6 (a) and again for memory slot 7 (b).
> =dec-a [9 2 10 [3 [0 6]] 0 5] > =dec-b [9 2 10 [3 [0 7]] 0 5] :: we can test our formulas by making a 5:: dummy core (a = 33, b = 77) :: first formula in battery just returns :: the current subject > =dummy-core [[[0 1] dec-gate] 33 77] > .*(dummy-core dec-a) 1032 > .*(dummy-core dec-b) 76
The recursion formula here operates by invoking its
subject—itself—and applying the dec-a and dec-b formulas to
it. Then we use opcode 9 for the new
subject’s setup: replace
payload with new a and b run the current core
> =recur [9 4 [[0 2] dec-a dec-b]] :: test it -- we want to see same battery, :: with payload being replaced with 32 and 76 5> .*(dummy-core recur) [[[0 1] [7 [0 3] 6 [5 [0 1] 1 0] [0 0] 6 [3 0 1] [0 0] 8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1] 0] 32 76] :: clean up the dummy-core > =dummy-core
The main logic is then:
:: check whether a is 0; return 2 if true :: else check whether b is 0; return 1 if true :: else recur > =main-logic [6 [5 [0 6] [1 0]] [1 2] [6 [5 [0 7] [1 0]] [1 1] recur]] 5 :: test (we aren't doing the equality case here) :: a < b > .*([[main-logic dec-gate] 9 10] [9 4 0 1]) 2 10:: a > b > .*([[main-logic dec-gate] 10 9] [9 4 0 1]) 1
We build an outer test for whether a==b, and then if it’s
not, we use the 1
opcode to return the core.
> =battery [main-logic dec-gate] :: payload for our core is memory slots 2 and 3 (a and b) > =comparison [6 [5 [0 2] [0 3]] [1 0] [9 4 [[1 battery] [0 2] 0 3]]] 5 :: test our 3 cases > .*([0 8] comparison) 2 > .*([0 0] comparison) 100 > .*([8 0] comparison) 1
We can take this code and use it anywhere that our subject is a cell of two numbers, and it will “just work".
[6 [5 [0 2] 0 3] [1 0] 9 4 [1 [6 [5 [0 6] 1 0] [1 2] 6 [5 [0 7] 1 0] [1 1] 9 4 [0 2] [9 2 10 [3 0 6] 0 5] 9 2 10 [3 0 7] 0 5] [7 [0 3] 6 [5 [0 1] 1 0] [0 0] 6 [3 0 1] [0 0] 8 [1 0] 8 [1 6 [5 [0 7] 4 0 6] [0 6] 9 2 [0 2] [4 0 6] 0 7] 9 2 0 1] 0] [0 2] 0 3]
One common convention used in languages like Hoon is to
denote Nock rules as constants, e.g. %0
(corresponding
to our 0). This
makes it much more straightforward to
interpret hand-rolled Nock code with addresses and constants
present.
After this tutorial, you should be prepared to interpret Nock
code when it is produced by Hoon. Although there is only
rarely any call to write Nock code directly, you should now
have a good understanding of how to read and interpret it. As
you write your own interpreters in the future, you may
even have call to hand-roll Nock expressions on occasion.

1Consult https://docs.urbit.org for details.⤴
3From this point on, we will write
Nock opcodes in special type so
that they can be distinguished from other numbers in Nock. This reflects
Hoon practice, which marks Nock rules as constants like %0. While not
strictly necessary, it can be helpful when learning or coding Nock to see
an explicit distinction.⤴
4Nock conventionally explains that there is one “true” case and (potentially) many “false” cases, thus 0/true and 1/false.⤴